Week 1
Powerpoint presentaton for Module 1 - View Online or Download
Extra Info - Number Systems (part 1)
Some Rules
ax
x = Exponent or Power.
ie: a2 = a x a, a3 =a x a x a, a6 = a x a x a x a x a x a, or 102 = 10 x 10 = 100
ax
x represents the base.
11110 indicates 111 in base 10, as opposed to 1112 which would represent 111 in base 2
In our everyday lives it is assumed that we are using Base 10 and thus we do normally attach the subscript to our numbers. However, when you are working with different number systems, it is important that you indicate which base you are using.
Highest digit used by a base
= Base -1
ie Base 10 uses digits {0..9}, Base 8 uses digits {0..7}
Power of 0
Any number to the Power of 0 = 1
ie 100 = 1, 160= 1, 1000 = 1
The Power of One
Any number to the power of 1 is equal to itself.
ie 101 = 10, 51 = 5
Highest Value that can be Represented
The highest value any group of digits can represent is BaseNo. of digits - 1
ie. the highest value 4 decimal digits can display is 9999
which is 104 - 1
the highest value 4 Binary digits can display is 1111 or 24 - 1 which is 1510.
Number of Values that can be Represented
The total number of values any group of digits can represent is BaseNo. of digits
ie. 1 Decimal digit can represent 101 or 1010 values: {0,1,2,3,4,5,6,7,8,9}
3 Binary digits can represent 23 or 810 values: {0,1,2,3,4,5,6,7}
8 Binary Digits can represent 256 unique values: 28 =256111111112 = 255. --> values 0..255 are represented, total = 256.
Decimal Numbers
The Decimal Number system uses the digits 0..9 to represent numeric values.
A digits place within a number indicates it's value.
For example:
107 |
106 |
105 |
104 |
103 |
102 |
101 |
100 |
Power of 10 |
|
100000000 |
10000000 |
1000000 |
10000 |
1000 |
100 |
10 |
1 |
Decimal value |
|
6 |
3 |
2 |
5 |
9 |
Example Decimal Number |
The number above 6325910 can be written in expanded form as follows:
| 9 | x | 100 | = | 910 |
|
| + | 5 | x | 101 | = | 5010 |
| + | 2 | x | 102 | = | 20010 |
| + | 3 | x | 103 | = | 300010 |
| + | 6 | x | 104 | = | 6000010 |
| = | 6325910 |
Binary Numbers
The Binary Number system has the digits 0 and 1 to represent values.
The position of a 1 or a 0 within a binary number determines it's value. For example:
210 |
29 |
28 |
27 |
26 |
25 |
24 |
23 |
22 |
21 |
20 |
Power of 2 | |
1024 |
512 |
256 |
128 |
64 |
32 |
16 |
8 |
4 |
2 |
1 |
Decimal value | |
1 |
0 |
1 |
0 |
1 |
1 |
Example Binary Number |
The above number (1010112) can be written in expanded form as follows:
| 1 | x | 20 | = | 12 |
|
| + | 1 | x | 21 | = | 102 |
| + | 1 | x | 23 | = | 10002 |
| + | 1 | x | 25 | = | 1000002 |
| = | 1010112 |
Converting Binary to Decimal
Method 1: Buy a good calculator.
Method 2:
1010112 (and any other binary number) can be converted into Base 10 or Decimal by using a table like the one above. The right most bit represents 1 x 20, and this equals 110, and so on.....
| 1 | x | 20 | = | 110 |
|
| + | 1 | x | 21 | = | 210 |
| + | 1 | x | 23 | = | 810 |
| + | 1 | x | 25 | = | 3210 |
| = | 4310 |
How can you convert numbers from decimal to binary?
Converting Decimal to Binary
The Division/Remainder Method
This method requires you to divide a Decimal* number by 2. The remainder - which obviously will be either a 1 or a 0 - is recorded. The quotient (the result) is then divided by 2 and it's remainder recorded, and so on until the quotient is zero (0). The remainders can then be written as a binary number in the order: the last remainder is the left most bit, the first remainder is the right most bit.
For example:
13010 converted to Base 2 or Binary
| 130 | / | 2 | = | 65 | r | 0 | ........... | 130 is divided by 2 and the remainder is recorded |
| 65 | / | 2 | = | 32 | r | 1 | ........... | The quotient from above is now divided by 2 |
| 32 | / | 2 | = | 16 | r | 0 | ||
| 16 | / | 2 | = | 8 | r | 0 | ||
| / | 2 | = | 4 | r | 0 | |||
| / | 2 | = | 2 | r | 0 | |||
| / | 2 | = | 1 | r | 0 | |||
| / | 2 | = | 0 | r | 1 | ........... | This remainder will be the left most bit |
Thus: 13010 = 100000102
*This method will allow you to convert Decimal numbers into any other number system
BCD
Short for binary-coded decimal, a format for representing decimal numbers (integers) in which each digit is represented by four bits (a nibble ). For example, the number 375 would be represented as:
0011 0111 0101
BCD is similar to hexadecimal format, the only difference being that hexadecimal uses the letters A-F to represent the digits 10-15 whereas BCD represents only the digits 0-9.
One advantage of BCD over binary representations is that there is no limit to the size of a number. To add another digit, you just need to add a new 4-bit sequence. In contrast, numbers represented in binary format are generally limited to the largest number that can be represented by 8, 16, 32 or 64 bits.
Binary fractions
How about fractions?
No one said we couldn't have negative powers of two!
21 |
20 |
2-1 |
2-2 |
2-3 |
2-4 |
Power of 2 |
2 |
1 |
0.5 |
0.25 |
0.0125 |
0.0625 |
Decimal value |
2 |
1 |
1/2 |
1/4 |
1/8 |
1/16 |
Fraction |
0 |
1 |
1 |
0 |
1 |
Example Binary Number |
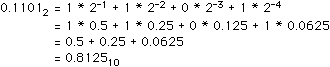
Binary to decimal - conversion is always exact
Decimal to binary - conversions are not always exact
Next section → Week 1 (part 2)