Week 1 - Number Systems (part 2)
- Octal Numbers
- Hexadecimal Numbers
- Binary / Hex Addition
- Fixed Length Numbers
- Compliment Numbers
- Fixed Length Arithmetic
Octal Numbers - Base 8 (digits 0 - 7)
85 |
84 |
83 |
82 |
81 |
80 |
Power of 8
|
||
32768 |
4096 |
512 |
64 |
8 |
1 |
Octal value
|
||
6 |
3 |
2 |
5 |
7 |
Example Octal Number
|
|||
| 7 | x | 80 | = | 710 |
|
| + | 5 | x | 81 | = | 4010 |
| + | 2 | x | 83 | = | 12810 |
| + | 3 | x | 85 | = | 153610 |
| + | 6 | x | 85 | = | 2457610 |
| = | 2628710 |
Converting Decimal to Octal
This can be done using the Division/Remainder Method except when converting to Octal you divide by 8 each time and record the remainder.
Converting from Binary to Octal
Converting from Binary to Octal is easy,simply group three binary digits together and represent as base 8.
ie 110011012 =
| ....Break the binary number into groups of three, starting from the right | |||
| ....Find the decimal value of each 3 bit number |
thus 110011012 = 3158
This process can be reversed to convert Octal Numbers into Binary.
Hexadecimal (digits 0 to 15, actually 0 to F)
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F | Hex |
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | Dec |
Hexidecimal requires 16 digits. This creates a problem as one cannot represent values greater than nine with just single digits. The solution was to find symbols to represent the values 10..15. A,B,C,D,E,F were chosen for this purpose and the complete set of Hex digits and their Decimal equivilants can be seen above.
165 |
164 |
163 |
162 |
161 |
160 |
||
65536 |
4096 |
4096 |
256 |
16 |
1 |
||
A |
B |
C |
|||||
| C | x | 160 | = | 1210 |
|
| + | B | x | 161 | = | 17610 |
| + | A | x | 163 | = | 256010 |
| = | 274810 |
Converting Decimal to Octal
This can be done using the Division/Remainder Method except when converting to Octal you divide by 8 each time and record the remainder.
Converting from Binary to Octal
Converting from Binary to Octal is easy,simply group three binary digits together and represent as base 8.
ie 110011012 =
| ....Break the binary number into groups of three, starting from the right | |||
| ....Find the decimal value of each 3 bit number |
thus 110011012 = 3158
This process can be reversed to convert Octal Numbers into Binary.
Binary numbers can be added just as you would with Decimal numbers, except of course that any sum greater than 1 will result in a carry.
Example:
011110 <-- carries
101101
+ 100111
overflow --> 1 010100
Hex addition
Add as if decimal numbers except:- if individual digits are A through F, convert to decimal equivalents and add
- if sum is greater than 16, replace sum with sum minus 16 and carry 1
- if sum is between 10 and 15 (decimal), replace sum with equivalent hexadecimal digit
D 13
+ C = + 12
$19 25
carries --> 1 1
DF6D
+ 246C
overflow --> 1 03D9
Examples of binary and hex addition
carries --> 11111
111011
+ 100111
overflow --> 1 100010
carries --> 1 1
11001
+ 01101
overflow --> 1 00110
1235
+ 567A
no overflow --> 68AF
carries --> 111
A9876
+ FDCA0
overflow --> 1 A7516
- Computer arithmetic is performed on data stored in fixed length memory locations, typically 8, 16, or 32 bits.
- No signed numbers (no sign bit)
Example conversions between number systems:
| Decimal | Binary | Hex |
| 255 | 1111 1111 | FF |
| 93 | 0101 1101 | 5D |
Special problems occur in manipulating fixed length numbers.
| Decimal | Binary | Hex | ||
201 |
= | 1100 1001 |
= | C9 |
+ 79 |
= | + 0100 1111 |
= | + 4F
|
280 |
= | 1 0001 1000 |
= | 1 18 |
overflow |
overflow |
The number 280 (base 10) is larger than the maximum 8-bit number; this results in a carry beyond 8 bits in the binary representation and a carry beyond two digits in the hexadecimal representation. When doing arithmetic using fixed length numbers, these carries are potentially lost.
How do you do negative numbers?
Signed magnitude
Use one bit for sign, 7 bits for number
Example: -1 (in an 8-bit system) could be 1000 0001 (base 2).
2's complement (most often used in computing)
Example: the 2's complement number representing -1 (in an 8-bit system) would be 1111 1111 (base 2).
Consider odometer numbers on a bicycle:
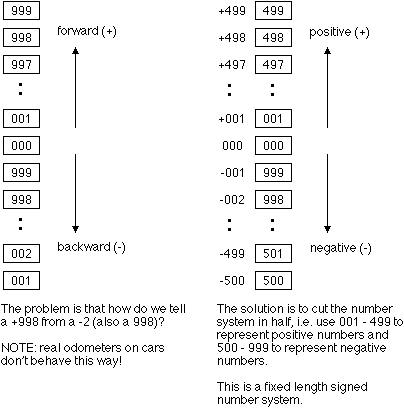
Decimal examples
Odometer numbers are useful for both addition and subtraction (complements) of signed numbers.
- 2 + 998
+ 3 + 003
+ 1 1 001
In the second example, the correct result is just the +001; the overflow is ignored in fixed-length complement arithmetic.
Do subtraction as addition by using complements, i.e.
A - B = A + (-B)
Important: It is easier to compute -B and add than to subtract directly.
Example:
- 005 + 995
+ 003 + 997
+ 008 1 992
signed 3-bit complement
+3 003
+2 002
+1 001
0 000
-1 999
-2 998
-3 997
-4 996
-5 995
-6 994
-7 993
-8 992
decimal 2's complement binary
+127 01111111
+126 01111110
+125 01111101
... ........
+2 00000010
+1 00000001
0 00000000
-1 11111111
-2 11111110
... ........
-127 10000001
-128 10000000
Why are these numbers called 2's complement?
M - N = M + (-N)
where -N is the complement of N.
Example:
decimal
+ 1 = 00000001
- 1 = + 11111111
0 = 1 00000000
2^8 - 1 11111111
- 27 - 00011011
11100100 corresponds to flipping all the bits;
also known as 1's complement
add 1 + 00000001
result 11100101 -27 in 2's complement representation
- Fixed-length nature of numbers stored in a computer
- More computationally efficient to implement a fast adder than an adder and a subtractor
Examples of 2's complement number operations
Addition and subtraction in 2's complement form- Addition: To compute N1 + N2, add N1 to N2
- Subtraction: To compute N1 - N2, add N1 to -N2
Examples:
decimal binary hex
11 = 00001011 = 000B
+ 21 = + 00010101 = + 0015
32 = 00100000 = 0020
21 = 00010101 = 0015
- 11 = + 11110101 = + FFF5
10 = 00001010 = 000A
11 = 00001011 = 000B
- 21 = + 11101011 = + FFEB
- 10 = 11110110 = FFF6
- 11 = 11110101 = FFF5
- 21 = + 11101011 = + FFEB
- 32 = 1 11100000 = FFE0
11 00001011
~11 - 11110100 1's complement
+ 1 + 00000001 add 1
-11 11110101 2's complement representation
An example in binary:
N 0000 0110 0100 0111
~N - 1111 1001 1011 1000 1's complement
+1 + 0000 0000 0000 0001 add 1
-N 1111 1001 1011 1001 2's complement representation
N 0647
~N - F9B8 1's complement
+1 + 0001 add 1
-N F9B9 2's complement representation
The Most Significant Bit (MSB) is the binary digit corresponding to the largest power of 2 and is always 1 for a negative 2's complement number. As a result it is often called the sign bit.
In 2's complement, -0 = +0. Technically, 0 is the complement of itself.
N 00000000
~N - 11111111 1's complement
+1 + 00000001 add 1
-N 00000000 2's complement representation
Problems With Fixed-Length Arithmetic
Overflow and underflow
For a 16-bit fixed-length number system,Adding signed numbers can easily exceed these limits.
first digit
0011 300016
0110 600016
1001 900016
Rule: If there is a sign change in adding two positive 2's complement numbers, then overflow has occurred.
Sign extension
How about if numbers are of different length? decimal 2's complement binary
3-bit 4-bit 8-bit
+3 011 0011 00000011
+2 010 0010 00000010
+1 001 0001 00000001
0 000 0000 00000000
-1 111 1111 11111111
-2 110 1110 11111110
-3 101 1101 11111101
-4 100 1100 11111100
Examples: Extend 9B16 to 16 bits.
9B16 = 1001 1011 = 1111 1111 1001 1011 = FF9B16
Extend 5F16 to 16 bits.
5F16 = 0101 1111 = 0000 0000 0101 1111 = 005F16
Adding two 2's complement numbers of different length
43A0 43A0
9B FF9B need to sign extend; you can't just add zeros.
???? 1 433B
Note that the 8-bit 9B16 and the 16-bit FF9B16 both represent -101 in their respective number systems.
Sources:
Baron and Higbie, "Computer Architecture", Addison-Wesley,1992,
Tanenbaum Andrew S, "Structured Computer Organization", Prentice-Hall,1990,
![]() Chapter 3 - Number Systems, Case Western Reserve University
Chapter 3 - Number Systems, Case Western Reserve University
Next section → Week 2